OpenRNG: New Random Number Generator Library for best performance when porting to Arm
OpenRNG the new open-source RNG optimised for Arm; easily port apps with a drop-in replacement for VSL RNG calls. Get the best performance on Arm.
By Kevin Mooney

We are thrilled to announce the first open-source release of OpenRNG, an open-source Random Number Generator (RNG) library, originally released with Arm Performance Libraries 24.04. This release comes in quick succession after we announced another new open-source library earlier in May this year, Arm Kleidi Libraries, for accelerating AI and Computer Vision. OpenRNG offers broad appeal, targeting performance improvements for AI frameworks and developers of scientific applications and financial software.
OpenRNG makes it easier to port applications to Arm by being a drop-in replacement for the random number generation component of Intel®’s Vector Statistics Library (VSL). VSL is shipped exclusively for x86 processors as part of OneMKL. As a great example of the performance uplift made possible, OpenRNG gives PyTorch’s dropout layer a 44x performance improvement over the existing implementation on Arm with minimal code changes. OpenRNG has also been shown to provide a 2.7x performance improvement over the C++ standard library.
Whilst initial optimizations are targeted at Arm-based systems, our intention is to grow OpenRNG to be a cross-platform project, and as such, we are accepting patches for any architecture.
We are grateful to Intel® for releasing this interface to us under a Creative Commons license. This license allowed us to implement this functionality for users of Arm-based systems, enabling software portability between architectures with no code changes.
The source code is now publicly available on Arm's Gitlab, and the documentation can be found in the Arm Performance Libraries Reference Guide.
Why are random numbers useful?
Random numbers are important across various applications for simulating inherently unpredictable natural processes. Examples include physics, where they are used for stochastic models of problems which are unassailable using deterministic models; finance, where they are used to model financial markets; and gaming, where they are used to implement AIs.
Physical processes and financial markets are complicated and have many inputs, making it impossible to understand, model, and predict them all. Instead, some inputs are treated as random variables that need to be generated quickly and repeatably; a bank's calculated exposure to risk should not change because rerunning an identical model gets different random numbers.
When developing an AI for a game, the movements and actions should not be predictable, so randomness is introduced. The faster randomness is generated, the more AIs can be generated simultaneously. Similarly, a multiplayer game needs the same random numbers generated on multiple devices. Different people would all need to see the baddies in the same place, randomness is important.
What's in the library?
OpenRNG implements several generators and distributions. Generators are algorithms that generate sequences that ‘appear random’ and have certain statistical properties, which we discuss below. Distributions map the sequences to common probability distributions, such as Gaussian or binomial.
OpenRNG also provides tools for duplicating and saving sequences and tools for distributing sequences among different threads. These tools enable features like efficient multithreading and checkpointing.
Random number generators
OpenRNG implements three types of random number generators:
- Pseudorandom number generators
- Quasirandom number generators
- Nondeterministic random number generators
Pseudorandom Number Generators (PRNG) are algorithms that generate sequences of numbers that appear statistically random but do so reproducibly. PRNGs typically pass many statistical tests for randomness, but once the current position in the sequence is known, the next number can be determined; this is why we say it appears random. OpenRNG implements many types of PRNG, such as linear congruential generators (LCG), multiple recursive generators (MRG), Mersenne twisters, for example MT19937, and counter-based generators, like Philox.
Quasirandom number generators (QRNG) are algorithms that generate low-discrepancy sequences. They fail statistical tests for randomness, but they fill spaces evenly by producing n-dimensional vectors that represent evenly distributed points on an n-dimensional hypercube. OpenRNG provides the SOBOL generator for generating low-discrepancy sequences.
Most modern hardware ships with nondeterministic random number generators, otherwise known as True Random Number Generators (TRNG), which OpenRNG provides a convenient interface for accessing. TRNGs can provide high-quality random numbers, sourcing their sequences from an external source. TRNGs are typically slower than PRNGs, and the sequences are not reproducible.
We have tried to ensure that the same generators and initializations are used as documented in the oneMKL documentation. This means that, where possible, the sequences are bitwise reproducible between OpenRNG and oneMKL.
Probability distributions
In addition to implementing RNGs, OpenRNG provides convenient methods for converting random sequences into common probability distributions. OpenRNG can generate random numbers with common probability distributions, both discrete and continuous.
A continuous distribution is any probability distribution over real numbers, for example, representable decimals between 0 and 1. Continuous distributions can be requested as single- or double-precision floating point numbers. OpenRNG supports many continuous distributions, including uniform, Gaussian, and exponential distributions.
A discrete distribution is any probability distribution confined to integers. OpenRNG implements common discrete distributions, such as uniform, Poisson, binomial, and Bernoulli.
The exact values generated by OpenRNG's distributions may differ slightly from those produced by oneMKL, as the precision of various operations differs between the two libraries.
Efficient multithreading
Long sequences of random numbers need to be generated for many applications. When running with multiple threads, having different independent sequences is important. OpenRNG supports this through a choice of two different methods: skip-ahead and leapfrog.
Skip-ahead advances the sequence by a given number of elements. Efficiency is important here, as it allows for skipping a large number of elements, for example, multiples of 232, and generating these all individually would incur a huge and unnecessary overhead.
The leapfrog method is intended for situations where the threads consume interleaved elements. For example, with n threads, the kth thread starts on the kth element of the 'global' sequence, and the ith element in that thread's sequence is the (k + i*n)th element of the 'global' sequence.
Performance
C++ standard library
The C++ standard library provides three generator types: linear congruential, Mersenne Twister, and subtract with carry. OpenRNG does not implement a subtract with carry generator, but it does implement linear congruential generators and Mersenne Twisters, so with a little configuration, we can compare an MCG31 and MT19937 implementation from both OpenRNG and the C++ standard library. The C++ standard library and OpenRNG have implemented many distributions in common, but we have chosen two ubiquitous distributions, the uniform distribution and the Gaussian distribution, also known as the normal distribution.
The chart below was generated with benchmark data from AWS Graviton 3 using GCC 14 and -O3. The benchmark consisted of repeatedly filling a buffer of 5000 elements and taking the ratio of the total time inside the hot loop for each library. We repeated this benchmark for all combinations of chosen generators and distributions.
For the uniform distribution, most of the runtime is spent generating the random sequence. The combination of the MCG31 generator with the uniform distribution realized the biggest speedup, with a ratio of 2.73.
For the Gaussian distribution, most of the runtime is spent transforming the random sequence to the Gaussian distribution. The biggest speedup over libstdc++ was a ratio of 1.88, using the MT19937 generator.
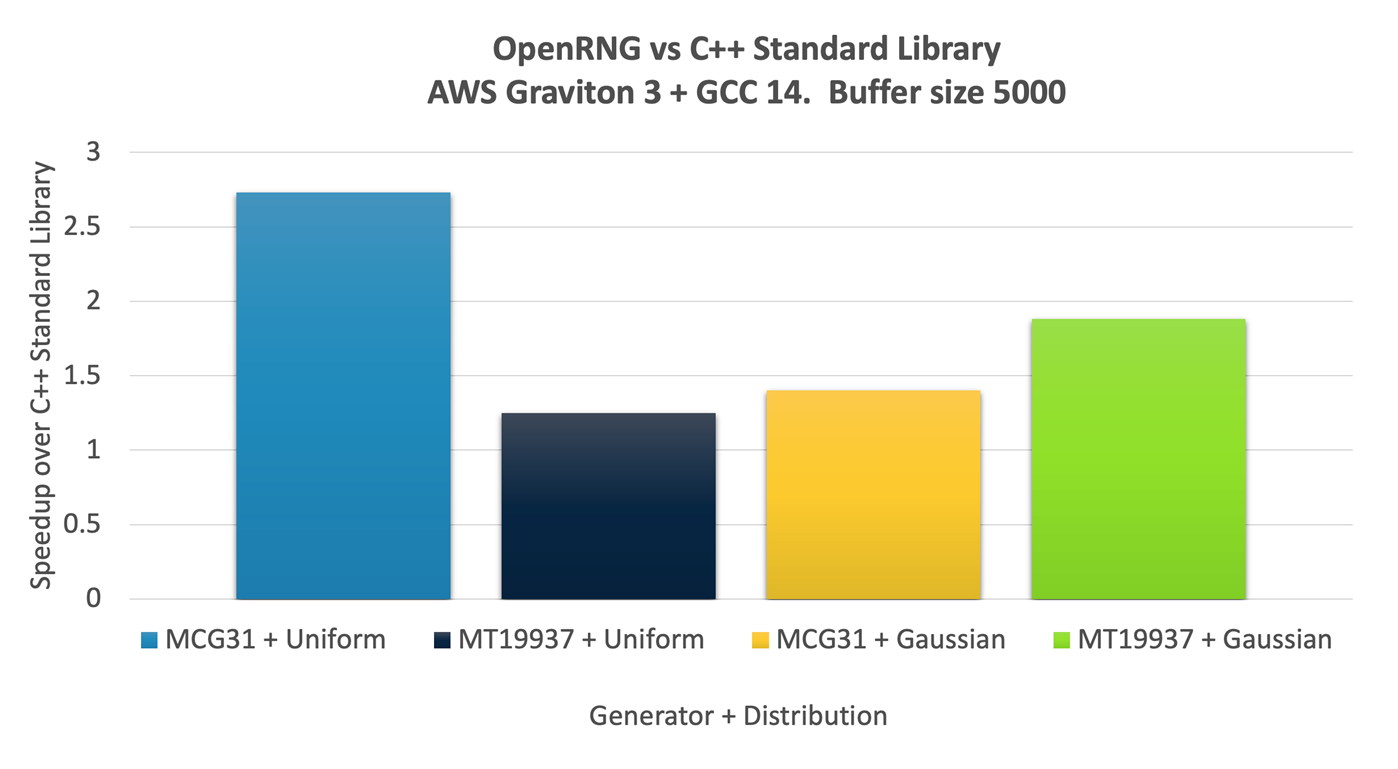
Bar chart showing the performance benefit of using OpenRNG instead of the C++ standard library. The height of each bar is the ratio of time spent generating random numbers with both libraries. Greater than 1 means OpenRNG was faster.
PyTorch
The following chart shows the benefit of having the VSL RNGs available on Arm for Machine Learning (ML) using PyTorch. PyTorch can be configured to use the VSL RNGs from OpenRNG as part of the dropout layer, drawing random values from a Bernoulli distribution. For example, for a batch size of 16, with an input tensor [16, 128, 3072], we see a 4x performance improvement when running sequentially compared with using the default RNGs within PyTorch. In addition, when the VSL interface is enabled, PyTorch uses skip-ahead to allow parallel generation of random values. If VSL is not used, the random values are always generated sequentially, without parallelism. Unlocking parallelism for the input tensor [16, 128, 3072] using 16 threads improves performance even further to around 44 times faster using OpenRNG than the default in the dropout layer.
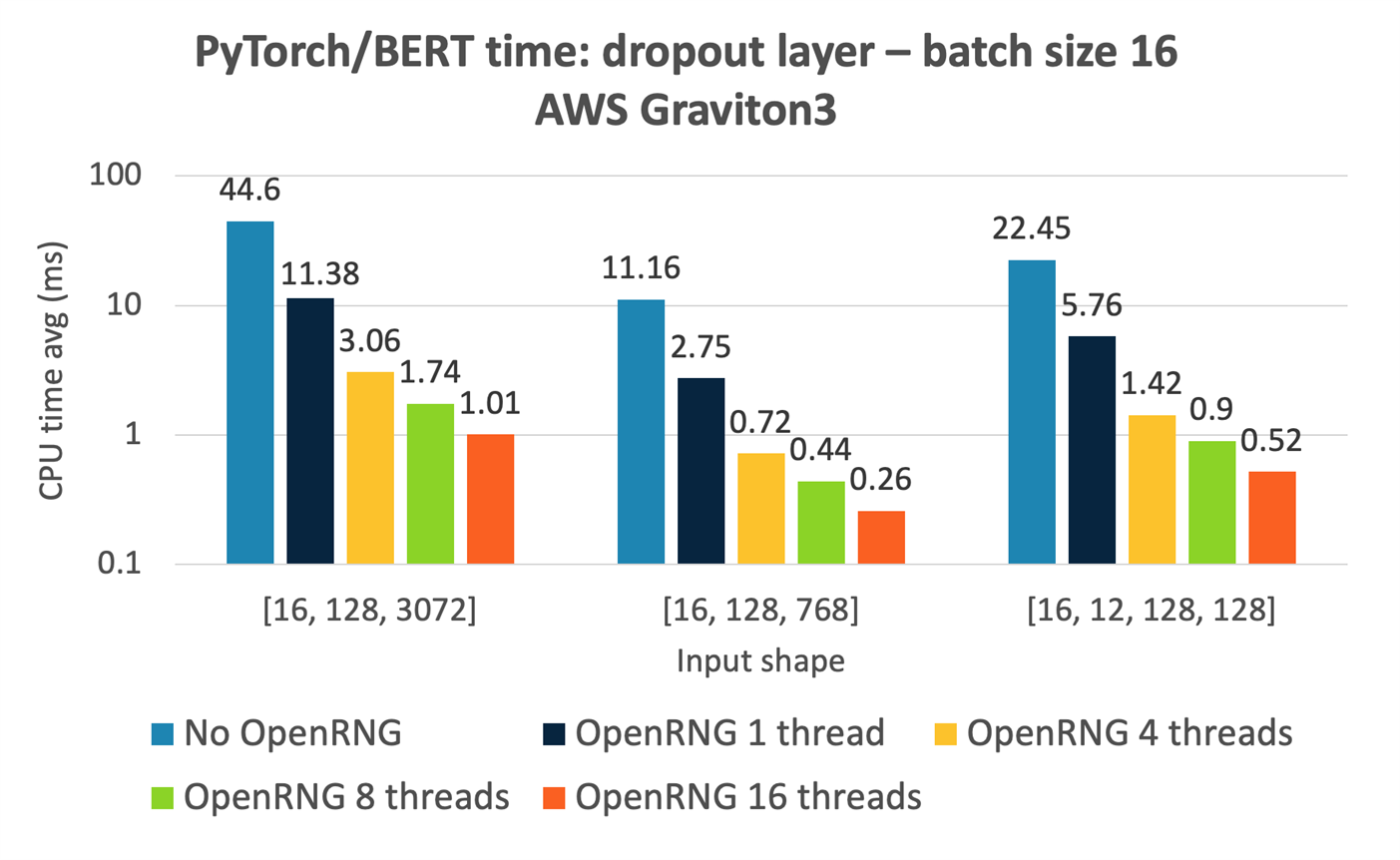
Bar chart showing the performance benefit of using OpenRNG with PyTorch. The height of each bar is the average time taken. A faster configuration will have a lower bar height.
Patches welcome!
Whilst we are pleased to release OpenRNG and have covered most of the functionality of VSL, some areas still require further development. There is a subset of functions that do not currently have implementations. In addition, today, all optimizations are exclusively targeted at Arm-based systems. However, we want OpenRNG to be a cross-platform project, so we accept patches for new reference implementations and performance optimizations for any architecture. If you would like to propose your own development work, report a bug, submit a feature request, or anything else, please get in touch by raising an issue on GitLab.
Arm Performance Libraries will continue to include OpenRNG in the future, tagging the released code in GitLab. The OpenRNG repository will be open for development throughout. Contributing guidelines are available on GitLab. We have tried to ensure that OpenRNG is permissively licensed with both MIT and Apache-2.0 so users can add the source to their own projects without burdensome restrictions.
By Kevin Mooney
Re-use is only permitted for informational and non-commerical or personal use only.
