Scalable MTJ simulation: How to efficiently analyze stochasticity in MRAM (2/2)
In part-two we continue to explore the simulation, characterization, and analysis of MRAM stochasticity, sharing a compact model and framework.

|
This post is co-authored by Fernando Garcia Redondo, Pranay Prabhat, and Mudit Bhargava. We would like to thank Cyrille Dray and Milos Milosavljevic for their helpful discussions. |
Magnetic-Random-Access-Memory (MRAM) Stochasticity, but how do MRAM cells work?
In part-one of this blog series, we introduced Magnetic-Random-Access-Memory (MRAM) technologies, and presented a compact model for the efficient simulation of MRAM cells in large-scale circuits.
MRAM is a Non-Volatile Memory (NVM) technology which is intrinsically stochastic. Translated to the circuit domain, the periphery surrounding the MRAM cell should be aware of this behavior, and designed to reliably write/read the MRAM cells incurring low Write/Read Error Rates (WER and RER respectively). Therefore, the circuit design relies on the accurate modeling and simulation of the stochastic behavior of MRAM cells.
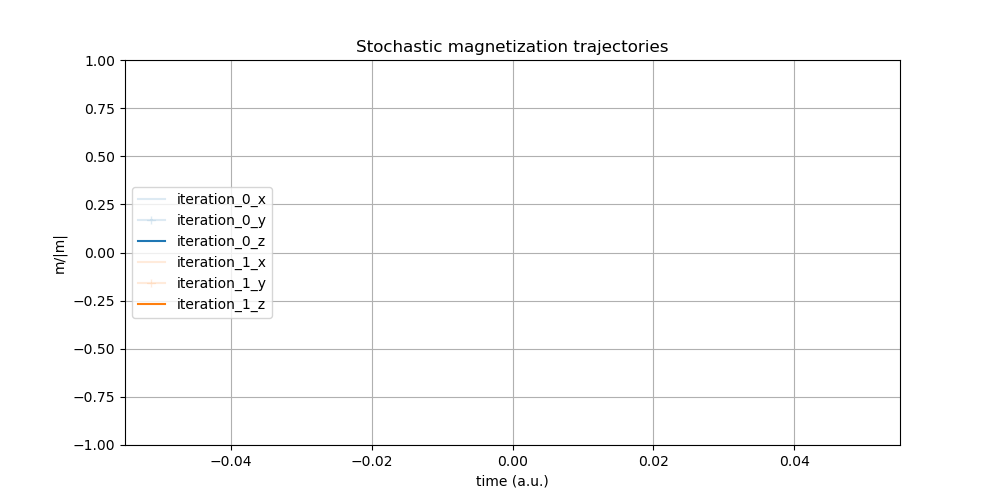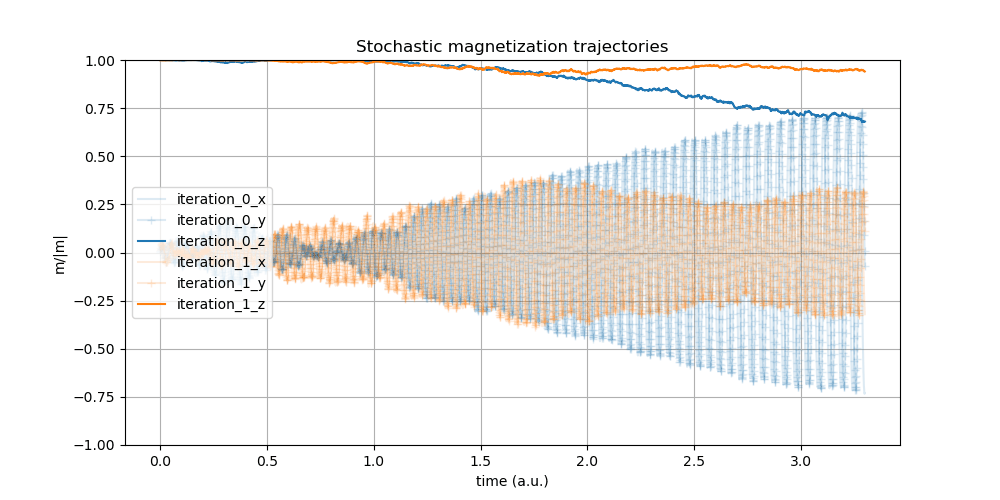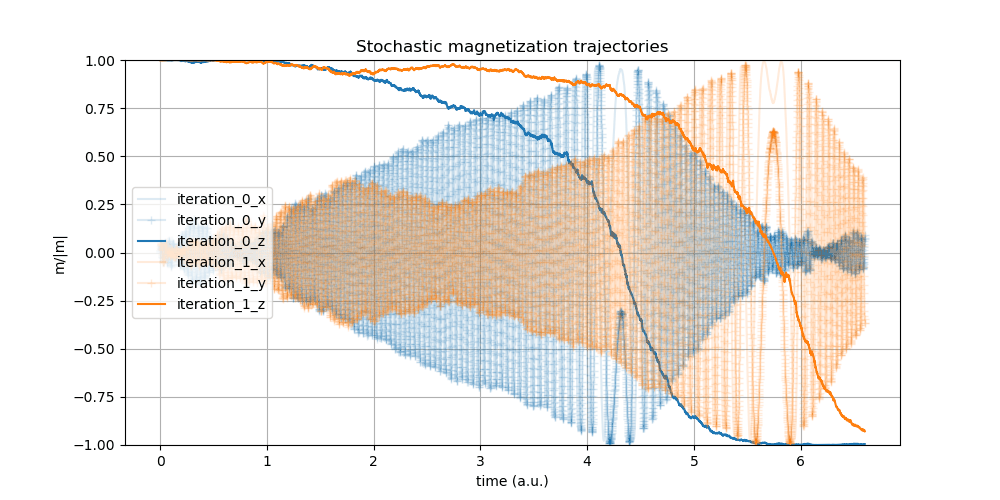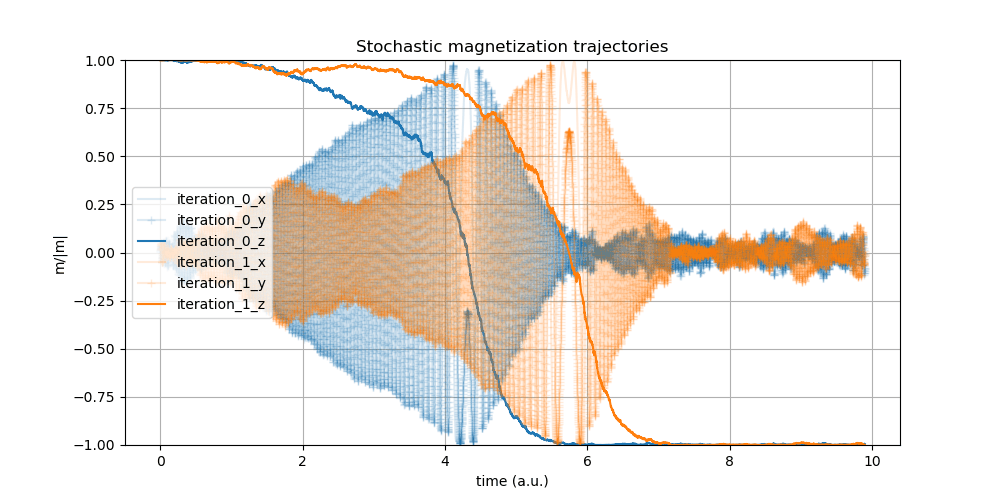
Figure 1: Stochasticity causes two different write operations in the same cell to behave differently.
In part one, we described how the simulation of stochastic differential equation (SDE) systems require the use of Ito or Stratonovich calculus [S. Ament, P. Horley]. Standard methods are not applicable, and the simulation of SDEs becomes a problem that involves a myriad of simulations using small time step, requiring huge computational resource.
We have developed an open-source framework for the simulation, characterization, and analysis of MRAM stochasticity. In this blog post, we introduce the stochasticity experiments. We also look at the analyses carried out and described in the related work "A Fokker-Planck Solver to Model MTJ Stochasticity" presented at IEEE European Solid-State Device Research Conference (ESSDERC) 2021. To calibrate the models for such stochastic based events, we implemented and analyzed two Fokker-Plank-Equation (FPE) solvers (numerical Finite Volume Method (FVM) and analytical). We then presented an optimization module that orchestrates the efficient computation of MRAM statistics and parameter regression.
“A Fokker-Planck Solver to Model MTJ Stochasticity”, or how to efficiently analyze stochasticity in MRAM
As seen in figure 2, the computation of WER with stochastic Landau-Lifshitz-Gilbert- Slonczewsky (s-LLGS) simulations requires a large number of random walks, especially for the low error rates (<< 1ppm) required for volume production.
For example, the simulation of 10,000 random walks solving the SDE using Stratonovich Heun algorithm in Cartesian coordinates system (0.1ps time step) for the write error rate computation seen in figure 2 took ~1150 hours. Taking advantage of the presented Python framework and multi-thread capabilities, this computation time was reduced to ~18 hours (64 threads). The characterization of a given MRAM cell for WER=1e-8 would require an unmanageable amount of time and computational resource.
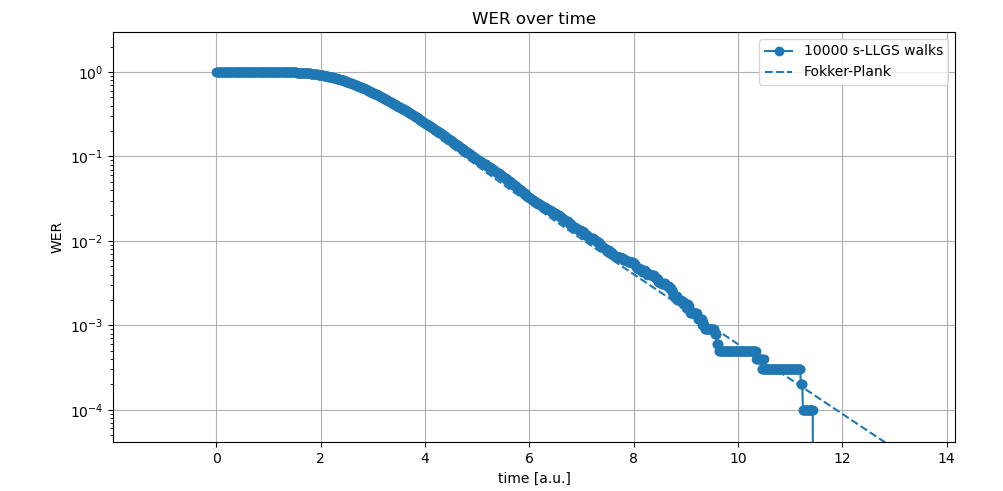 Figure 2: WER simulations comparing FPE and s-LLGS approaches.
Figure 2: WER simulations comparing FPE and s-LLGS approaches.
To alleviate this issue, SDE tools, such as the FPE, statistically analyze the Magnetic Tunnel Junction (MTJ) magnetization and provide a simplified solution with sufficient accuracy to analyze such error rates [Tzoufras], [Y. Xie], [W. H. Butler]. Compared against a set of s-LLGS random-walk transient simulations, the FPE accurately evolves an initial MTJ magnetization probability through time based on the current and external fields. Instead of independent transients, the FPE computes the probability distribution of the magnetization at a given point in time, capturing the statistical behavior of the MTJ cell. Taking advantage of the open-source framework described in the next section, the Fokker-Plank WER computation was solved in seconds.
This computational resource problem magnifies when the compact model designer needs to find the MRAM parameters that best fit a measured statistical behavior, traditionally multiple WER at given current or pulse width points. The number of required s-LLGS random walks multiplies, making the required fitting impossible.
To address this issue, we present an open source stochastic framework for the characterization and analysis of MRAM stochastic effects. With the proposed solution, we can generate WER/RER in seconds. This efficient analysis enables, for the first time, the fitting of the complex set of MRAM parameters onto such heterogeneous data points. We will also introduce the mechanisms and tools that, solving the stochastic Fokker-Plank differential equation, allowed us to regress the set of physical parameters that best fit a collection of Error Rate points as a function of a current pulse width and published foundry data.
Fokker-Plank equation
The advection-diffusion or Fokker-Plank equation has been widely used to analyze the evolution over time of the probability density function of the magnetization of an MRAM cell:
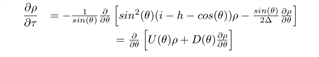 Figure 3: Fokker-Plank equation.
Figure 3: Fokker-Plank equation.
This FPE can be solved numerically through finite differences (FDM), FVM or analytical solutions. Even though solving the FPE numerically through FDM or FVM has significant advantages over solving myriads of s-LLGS random walks, the computational cost of simulating large MRAM switching related to low current operation modes could still be significant. As described in figure 4, we characterized:
- The computational load required to simulate a single s-LLGS stochastic random walk
- The different FVM FPE simulations using different time and spatial resolutions
- The various analytical FPE simulations varying the number of coefficients of the expansion series used.
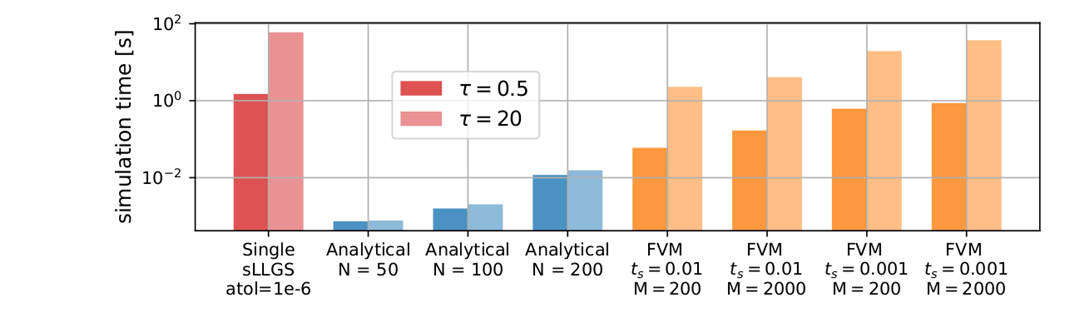 Figure 4: Computational load comparison of a single s-LLGS random walk and different FPE solvers.
Figure 4: Computational load comparison of a single s-LLGS random walk and different FPE solvers.
First, it can be clearly seen how computing millions of s-LLGS is simply unmanageable. Second, while FVM FPE approaches are a good method for a small number of WER/RER computations, should multiple simulations be required a faster method is required. This is the case for the design space exploration occurring during the fitting of MRAM parameters, where the faster yet more accurate analytical solutions approach is required.
It is important to highlight that even FVM FPE solutions constitute a reasonable solution to enable statistical analyses that would otherwise be impossible using billions of s-LLGS, as the simulation time is directly proportional to the write pulse width being simulated. Therefore, the characterization of low-current regimes requires longer simulated times, which still involve huge computational resources. On the contrary, the analytical FPE approach requires constant time to simulate longer pulse widths.
Presented solution framework
Complementing the compact model and simulation framework that enables the efficient simulation of circuits with MRAMs, the MRAM characterization framework focuses on the MRAM behavior statistical analysis. The presented framework is comprised of two FPE solvers: a FVM solver for validation purposes and a fast analytical solver that can compute the magnetization probability at any required time in mere milliseconds. To support these two solvers, we developed an Error Rate (WER/RER) computation script, which computes and digests the current/switching time ER curves in seconds. Finally, we included a third key module in the stochastic framework, an optimizer based on Scipy optimization tools that handles the parameter regression.
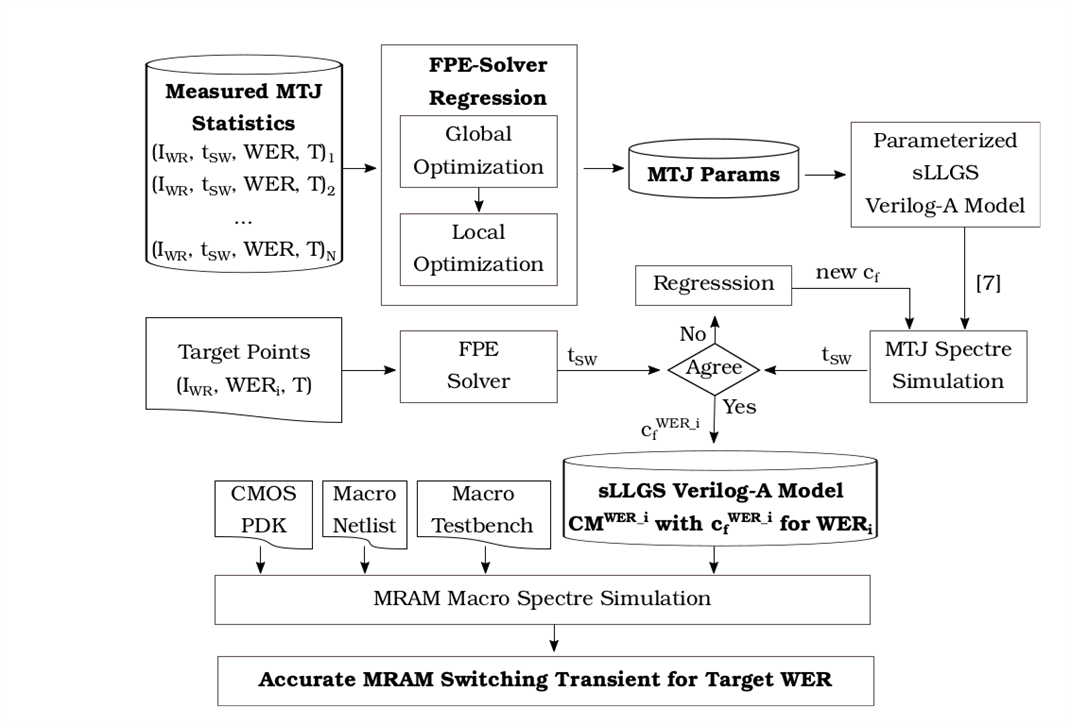
Figure 5: Proposed framework and methodology.
At the end of the process, the circuit designer obtains a set of MRAM compact models, ready to be simulated in traditional circuit simulators, that have been accurately calibrated to represent an MRAM matching significant stochastic behaviors - mean behavior, WER 1E-6, WER 1E-8.
As an example, we take the two stack processes presented in [G. Hu], where a set of points are provided. First the most computing intensive task takes place, regressing the MRAM parameters that best describe the provided stochastic behaviors. Our framework finds the proper parameters in a reasonable timeframe (~1000 CPU hours), a task which would otherwise be completely impossible using s-LLGS simulations, and much slower (almost impractical) using FVM approaches.
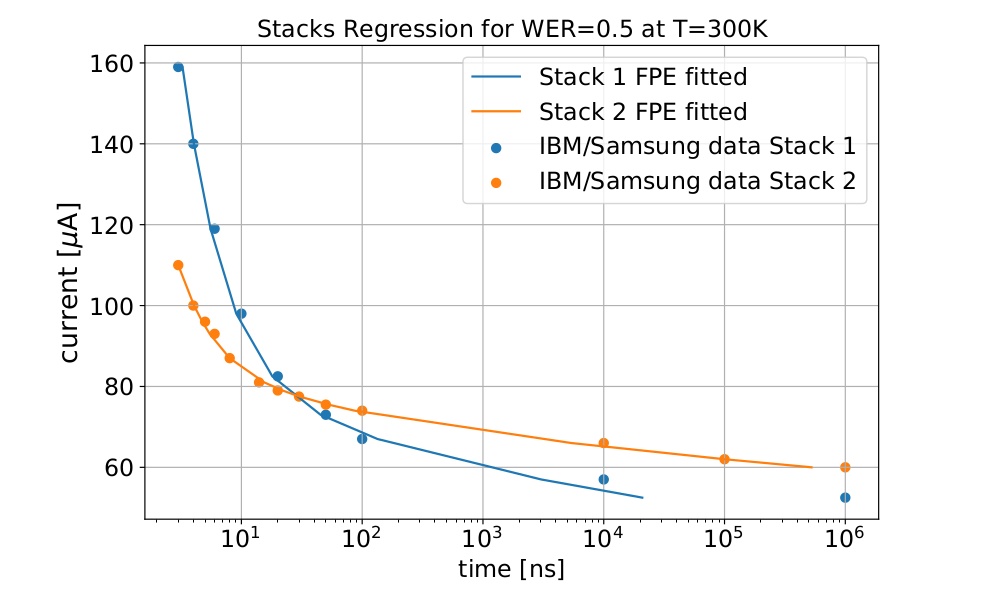 Figure 6: Current/switching time fitting for two MRAM stack processes without any prior knowledge.
Figure 6: Current/switching time fitting for two MRAM stack processes without any prior knowledge.
Once we know the MRAM stack parameters, we can directly analyze its statistical behavior under any writing conditions, and obtain the WER analyses at multiple writing. As an example, looking at the results presented in figure 7, we as circuit designers can note how Stack 2 is characterized by an easier write-ability, requiring less time to switch in the same current.
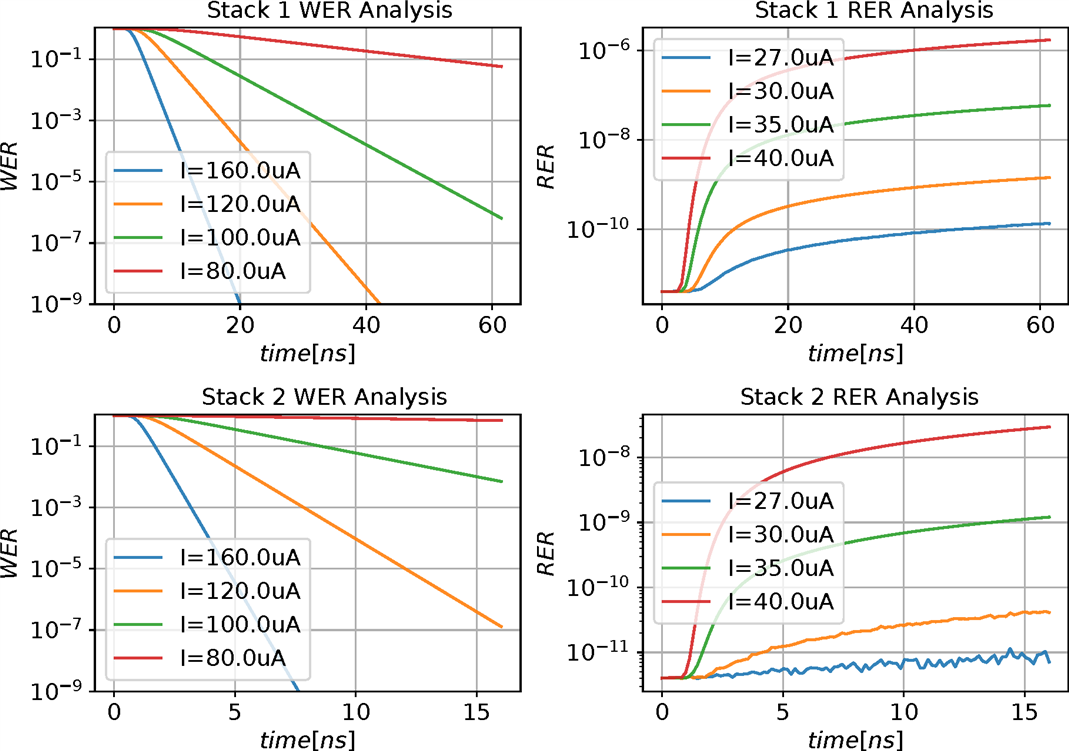
Figure 7: Current/switching time fitting for two MRAM stack processes without any prior knowledge. Note timescale differences in x-axes
Finally, following the methodology described in figure 5, and complementing the compact model presented in “A Compact Model for Scalable MTJ Simulation” (which is also included in the open source framework), with the physical parameters we found that we can compute the H_fth parameters that enable circuit designers to accurately simulate the required MRAM cell at the significant WER statistical events. With the Verilog-A model completely parameterized, the circuit designer can simulate the full memory circuit, analyzing its timing or its power consumption at the required significant events. As an example, figure 8 describes the switching in an MRAM cell through the evolution of the magnetization vector. The graph shows the the mean behavior (represented by the time that it takes for 50% of the writing occurrences to flip the cell at a given current) and the WER 1E-6 and WER 1E-8 switching (the time that it takes to flip the cell for all but one of occurrence in 10E6 and 10E8 writing operations).
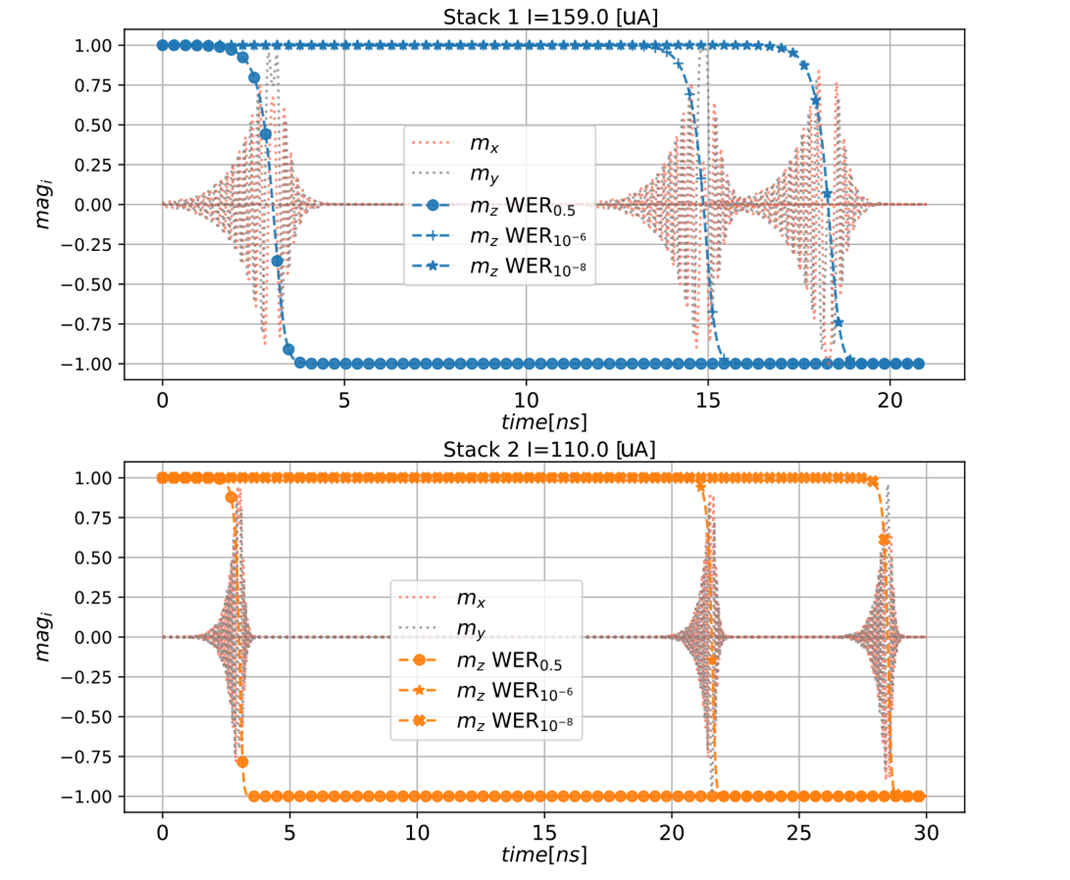
Figure 8: Simulation of different statistically significant events on the same MRAM cell.
An overview of Arm’s MRAM simulation framework
In this series of posts, we presented our open-source framework for the characterization and analysis of MRAM stochasticity, and a compact model and framework for the efficient and scalable simulation of circuits with MRAMs.
We provided Verilog-A and Python compact models, able to emulate the behavior of MRAMs switching at significant statistical events. To calibrate the models for such stochastic events, we implemented and analyzed two FPE solvers (numerical FVM and analytical), and presented an optimization module that orchestrates the efficient computation of MRAM statistics and parameter regression.
Therefore, the open-source framework provides circuit designers with the tools and models required to create the next generation of MRAM based circuits, and brings MRAM model researchers the statistical tools required to study the MRAM stochastic behavior.
Explore open source framework Questions? Contact Fernando
The following frameworks have been presented:
- A Compact Model for Scalable MTJ Simulation, IEEE International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design, SMACD 2021.
- A Fokker-Planck Solver to Model MTJ Stochasticity, European Solid-State Device Research Conference, ESSDERC 2021.
Glossary
|
Abbreviation |
Expanded |
|
TMR |
Tunnel-Magneto-Resistance |
|
MRAM |
Magnetic-Random-Access-Memories |
|
STT |
Spin-Transfer-Torque |
|
NVM |
Non-Volatile Memory |
|
MJTs |
Magnetic Tunnel Junctions |
|
FL |
Free Layer |
|
PL |
Pinned Layer |
|
P State |
Parallel State |
|
AP State |
Anti-Parallel State |
|
s-LLGS |
Stochastic Landau-Lifshitz-Gilbert- Slonczewsky |
Re-use is only permitted for informational and non-commerical or personal use only.
